Reinforcement Learning Basics: Deep Deterministic Policy Gradient Method (DDPG)

In earlier posts, we explored value-based methods (like DQN) and policy gradients (like REINFORCE, A2C) — but all of these target discrete action spaces. Many real-world problems, especially in robotics or control systems, require actions to be continuous, like adjusting a throttle or steering angle.

This is where the Deep Deterministic Policy Gradient (DDPG) algorithm shines, introduced by Lillicrap et al. (2015). In this blog we will implement this method for MountainCarContinuous environment of gym.

1. What is Deep Deterministic Policy Gradient Method?

DDPG is an off-policy, actor-critic algorithm designed to handle continuous action spaces, combining the stability of DQN with the flexibility of policy gradients. As the name suggests, the policy we are trying to learn is deterministic that is the network does not include any stochasticity. 

The design of the network is similar to previously seen A2C method. However, in this case, being off policy its more sample efficient. The actor network estimates the policy or actions to be taken and the critic network estimates the Q-Values.

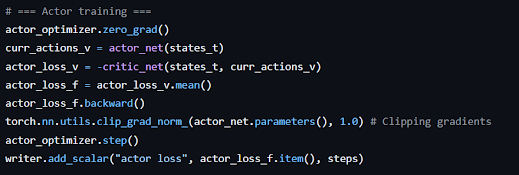
The critic update is similar to the A2C as discussed in the previous blog. However, the actor loss is a bit different. It is such that it maximizes the critic estimate.

Actor Loss

where:

Qw​(s,μθ​(s)) is the Q-Val predicted by critic for current deterministic policy and state(s)

2. Ornstein-Uhlenbeck Noise

 In reinforcement learning with continuous actions, naive exploration (like adding uncorrelated Gaussian noise) can cause the agent’s actions to fluctuate wildly from one step to the next. This leads to jerky, unrealistic behaviors — especially problematic in tasks that require smooth control, like robotics or driving.

To solve this, Ornstein-Uhlenbeck (OU) noise is used as a temporally correlated exploration process. Instead of sampling each action’s noise independently, OU noise generates smooth, continuous fluctuations over time, better mimicking realistic action changes.

OU Noise Equation

where:

xt is the Noise at time t.

$\sigma \mathcal{N}(0,1)$, adds Gaussian noise scaled by $\sigma$.

θ is the constant which represents a mean reversion speed.

μ is the mean. (mostly taken as zero).

This process models the velocity of massive Brownian particle under the influence of friction.

3. Soft Update/Polyak Averaging

In deep reinforcement learning algorithms like DDPG, target networks are used to stabilize training by providing slowly moving targets for value updates. Rather than instantly copying the weights of the main networks (hard update), soft updates adjust the target networks gradually.

This prevents sudden, destabilizing changes and smooths learning.

Polyak Averaging Equation

where:

• $\theta$ is the parameter of the main (actor or critic) network,

• $\theta'$ is the parameter of the target network,

• $\tau \in (0, 1)$ is the soft update coefficient, typically a small value like 0.005.

4. The Mountain Car Environment

The MountainCarContinuous-v0 environment is a classic benchmark from OpenAI Gym designed to test continuous control algorithms. The agent controls a car positioned in a valley, with the goal of building enough momentum to drive up the steep hill on the right and reach the flag. Since the car’s engine is underpowered, it must learn to swing back and forth to accumulate speed. The action space is continuous, requiring the agent to output smooth, precise throttle signals, making this environment ideal for testing algorithms like DDPG that operate in continuous action spaces.

5. The Training Loop

• Initialize the hyperparameters, networks and replay buffer.
• Play episodes till replay buffer reaches a particular point. Store (s, a, r, s_next, done).
• Sample a batch from experience replay buffer.
• Calculate the critic loss and backpropagate.
• Calculate the actor loss and backpropagate.
• Soft update the target nets.
• Test the current actor network
• Repeat the process till convergence.

6. Implementation

The main highlights of the code are:

1. The Network: The actor net and the critic network are defined separately as shown in the flowchart. 
   
   
   
2. Play: Collect at least 50,000 states and store it in the replay buffer. Sample a batch of 64 samples.
3. Critic Training: Calculate the critic loss and perform the backpropagation.

   

   
   
4. Actor Training: Calculate the actor loss and perform the backpropagation.

   

   
   
5. Soft-Update:  Sync the target networks by performing Polyak Averaging.

   

   
   

The code can be found in this repository. I have tried my best to make it as clear as possible, so that the theory can be closely followed.

Code: DDPGM

It takes around 80 min for convergence on my GTX 1650 card.

6. Conclusion

Deep Deterministic Policy Gradient (DDPG) is a powerful algorithm enabling end-to-end learning of continuous control policies, making it foundational in robotics and control RL research. While sensitive to hyperparameters, DDPG laid the groundwork for later algorithms like Twin Delayed DDPG (TD3) and Soft Actor-Critic (SAC), which address DDPG’s limitations.

Understanding DDPG is a crucial milestone for anyone diving into continuous action reinforcement learning. Thank You and Stay Tuned.

FUTURE BEYOND OUR STAR!